logo
GrainRain
banner
NEWS LETTER

动态规划进阶 | 常见题型总结

Scroll down

进阶动态规划与常见题型

包含：区间 $\rm dp$, 树形 $\rm dp$, 状压 $\rm dp$, 计数 $\rm dp$, 数位 $\rm dp$, 以及其他有一定难度的状态设计.

区间 $\rm dp$

石子合并

将若干个集合合并为一个集合, 每次合并付出一定代价, 求将所有集合合并为一个集合所付出的最小代价

考虑设 $f_{i, j}$ 表示将所有从第 $i$ 个集合到第 $j$ 个集合合并为一个集合的合并方式

状态表示

我们可以发现, 不论哪种合并方式, 最后一步均为将两个集合合并为一个集合, 因此可以以最后一次合并集合的分界线分类, 即可以将全集分为 $k - 1$ 个部分

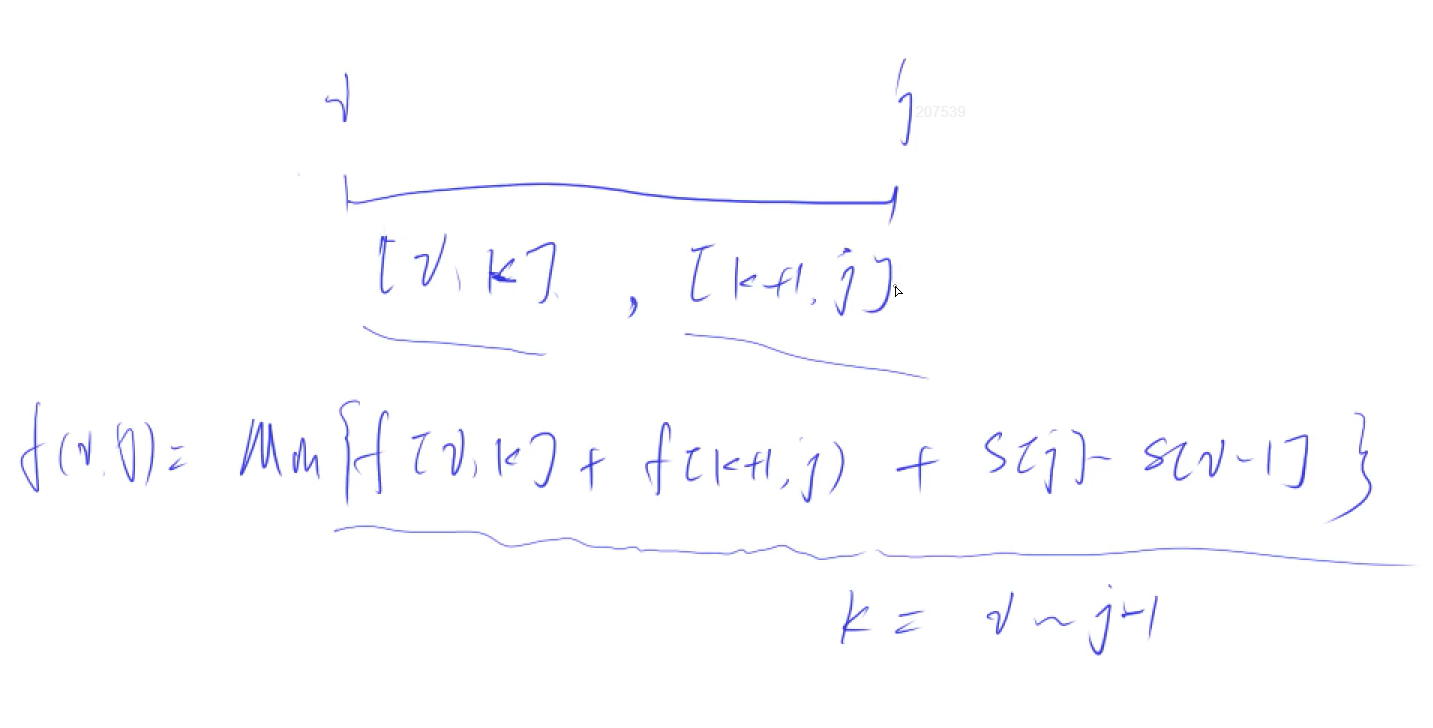
由此, 第三维度的 $k$ 仅需从 $1$ 枚举到 $j - 1$ 即可

时间复杂度分析

状态的二维转移需要 $O(n^2)$, 枚举 $k$ 的时间为 $O(n)$, 因此总时间复杂度为 $O(n^3)$

$Solutions$

先从小到大枚举区间长度, 再从前往后枚举区间左端点, 最后枚举分割点的决策

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int n;
int s[N], f[N][N];
// s 存储前缀和

cin >> n;
for (int i = 1; i <= n; i ++) cin >> s[i];
for (int i = 2; i <= n; i ++) s[i] += s[i - 1]; // 处理前缀和

for (int len = 2; len <= n; len ++) // 枚举待合并的区间长度
    for (int i = 1; i + len - 1 <= n; i ++) { // 枚举区间位置
        int l = i, r = i + len - 1; //  取出起始位置 
        f[l][r] = INF; // 初始化一个最大值, 循环找出最小值 
        for (int k = l; k < r; k ++)
            f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
        // 按合并区间的分界线分类枚举 
    }
cout << f[1][n] << endl;

树形 $\rm dp$

典例 $1$ - 树的直径

简化题意

给定一棵树, 要求在 $O(n)$ 时间内求树的直径, 直径定义为树上任意两节点之间最长的简单路径.

$Solution$：

尝试按边权分为两种情况：

1.当边权恒定时：
  1. 任取一点作为起点, 找到距离该点最远的一个点 $u$
  2. 找到距离 $u$ 最远的一个点 $v$
证明：

如需证明该方法的正确性, 只需证明任取一点 $a$ , 距离 $a$ 最远的一个点一定是树的一条直径的端点(起点)

假设任取一点 $a$ , 距离 $a$ 最远的一个点 $u$ 不是树的一条直径的端点. 取出该树的直径 $bc$, 由于树整体连通的特性, $a$ 点一定可以到达 $c$ 点. 则会出现以下几种情况：

  1. $au$ 与 直径 $bc$ 相离

    在两条边上分别任取两点 $x$ $y$ 如图

    在上图中, 我们可以发现 $bu$ 两条边比直径更大, 不符合题意

  2. $au$ 与 直径 $bc$ 相交

    由于 $u$ 是距离 $a$ 最远的点, 所以边 $1$ 一定大于边 $2$, 因此我们又找到了一条比直径更长的边, 不符合题意

2.当边权为任意实数时：

Acwing1072 - 树的最长路径

集合表示

在树中随意选择一个节点作为根节点, 将全集按照高度最高的点分类, 枚举时依照点枚举, 表示在当前点作为当前路径最高点的情况中路权最大值

如果求一个点作为当前路径最高点的情况中路径的最大值, 只需提前处理它的子节点作为当前路径最高点的情况, 从中取路权最长值与次长值, 相加即为该点的路权最大值

$Code$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
int dfs(int u, int father){
// 返回从当前点向下搜索的最大长度  
// fahter 防止 dfs 反向搜索
	int dist = 0;
	int d1 = 0, d2 = 0;
	// 表示以当前节点为起始位置, 向下搜索的最长距离与次长距离 
	
	for (int i = head[u], j; ~i; i = edge[i].nxt) {
		j = edge[i].to;
		if (j == father) continue;
		int d = dfs(j, u) + edge[i].w;
		dist = max(dist, d);
		
		if (d >= d1) d2 = d1, d1 = d;
		else if (d > d2) d2 = d;
		// 对最大值和次大值进行维护 
	}
	ans = max(ans, d1 + d2);
	return dist;
}

int main() {
	memset(head, -1, sizeof head);
	cin >> n; 
	for (int i = 0; i < n - 1; i ++) {
		int x, y, z;
		cin >> x >> y >> z;
		add(x, y, z);
		add(y, x, z);
	}
	dfs(1, 0);
    // 传入 father 参数, 防止向反方向前进导致 TLE
	cout << ans << endl;
	return 0;
}

扩展: 寻找直径必经边 SDOI2013 直径

典例 $2$ - 树的中心

简化题意

给定一棵树, 找一个点使得该点到树中其他结点的最远距离最近.

$Solutions$

分别维护每个点到其他节点的最长距离, 在所有点的最远距离中取最小值

对于一个节点到其他点的最长距离, 可以分为以下几类：

  1. 向下行进的边
    类似于 树的重心中的处理方式, 维护向下距离 $dist$ 即可
  2. 向上行进的边
    将该边分成两个部分, 从该点向上行进到点 $u$ , 再判断 该点的 $dist$ 是否经过当前点
    1. 未经过当前点, 加上 $dist_u$ 即可
    2. 走过当前点, 加上次长路径(除去当前值所在的子树)

$Solutions$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
int n;
int d1[N], d2[N];
// d1 表示从该点向下行进的最长距离
// d2 表示从该点向下行进的次长距离 
int up[N];
// up 表示从当前点向上行进的最长距离 
int p1[N], p2[N];
// 用于存储最长边和次长边由哪里转移而来 

int dfs_d(int u, int father) {
// 求从 u 点向下走的最长路径 
	d1[u] = d2[u] = -INF; // 为对实数边权进行处理, 初始值赋为负无穷
	for (int i = head[u], j; ~i; i = edge[i].nxt) {
		j = edge[i].to;
		if (j == father) continue; // 如果该点是向上搜索的, 那么直接跳过
		int d = dfs_d(j, u) + edge[i].w; // 取出向下的最长距离 
		if (d >= d1[u]) {
			d2[u] = d1[u], d1[u] = d;
			p2[u] = p1[u], p1[u] = j;
		} else if (d > d2[u]) d2[u] = d, p2[u] = j;
	}
	if (d1[u] == -INF) d1[u] = d2[u] = 0; // 对于叶节点的特殊处理 
	return d1[u];
}

void dfs_u(int u, int father){
	for (int i = head[u], j; ~i; i = edge[i].nxt){
		j = edge[i].to;
		if (j == father) continue;
		if (p1[u] == j) up[j] = max(up[u], d2[u]) + edge[i].w;
		//  最长路径由该节点所在子树转移而来, 则使用次大值 
		else up[j] = max(up[u], d1[u]) + edge[i].w;
		dfs_u(j, u);
	}
}

int main() {
	memset(head, -1, sizeof head);
	cin >> n;
	for (int i = 0, x, y, z; i < n - 1; i ++) {
		cin >> x >> y >> z;
		add(x, y, z), add(y, x, z);
	}
	
	dfs_d(1, -1); // 向下搜索 
	dfs_u(1, -1);
	
	int res = INF;
	for (int i = 1; i <= n; i ++)
		res = min(res, max(d1[i], up[i]));
	cout << res << endl;
	return 0;
}

典例 $3$ - CF685B - 树的重心

简化题意

给定一棵树和若干询问, 询问以 $x$ 为根节点的子树的重心

对于树上的每一个点, 计算其所有子树中最大子树的节点数, 这个值最小的点就是这棵树的重心.

$Solution$

首先我们需要了解树重心的性质：

  1. 以树的重心为根时, 所有子树的大小都不超过整棵树大小的一半.

  2. 树中所有点到某个点的距离和中, 到重心的距离和是最小的（如果有两个重心, 那么到它们的距离和相同）.

  3. 把两棵树通过一条边相连得到一棵新的树, 那么新的树的重心在连接原来两棵树的重心的路径上.

  4. 在一棵树上添加或删除一个叶子, 那么它的重心最多只移动一条边的距离.

考虑先维护 $core_i$ 表示以 $i$ 为根节点的子树重心, 再进行离线访问

当枚举点 $x$ 的所有子树 $y$, 若 $x$ 的子树重心在 $y$ 子树中, 则一定在 $y$ 子树重心上方

因此, 我们维护指针 $pos$, 不断从 $y$ 子树重心向上跳, 并进行更新即可

发现 $pos$ 最多只会将每个点遍历一次, 因此预处理时间复杂度可以做到 $O(n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int father[N], siz[N], mx[N], core[N];
// 维护每个点的祖先, 以当前点为根的子树大小, 最大的子树大小

void dfs(int root) {
	siz[root] = 1;
	for (int i = head[root], j; ~i; i = edge[i].nxt) {
		j = edge[i].to;
		dfs(j);
		siz[root] += siz[j];
		mx[root] = max(mx[root], siz[j]);
	}
	
	int id = root, mn = mx[root];
	for (int i = head[root], j; ~i; i = edge[i].nxt) {
		j = edge[i].to;
		int step = core[j], val = max(mx[step], siz[root] - siz[step]);
		int pos = step;
		while (father[step] != root) {
			step = father[step];
			int nw = max(mx[step], siz[root] - siz[step]);
			if (nw < val) val = nw, pos = step; // update
			else break;
		}
		if (mn > val) mn = val, id = pos;
	}
	core[root] = id;
}

典例 $4$ - 最大独立集问题：没有上司的舞会

简化题意

在树中选带权点, 使得任意两个点都不相邻, 求最大权值

$Solution$

考虑设 $f_{i, 0/1}$ 表示是否选择 $i$ 这个点, 任选一个入度为 $0$ 的点, 依据当前点的状态更新连向点的状态, 并递归处理. 

1
2
3
4
5
6
7
8
9
void dfs(int root) {
	f[u][1] = r[u], f[u][0] = 0;
	for (int i = head[u], j; ~i; i = edge[i].nxt){
		j = edge[i].to;
		dfs(j);
		f[u][1] += f[j][0];
		f[u][0] += max(f[j][1], f[j][0]);
	}
}

状压 $\rm dp$

经典模型

旅行商问题：吃奶酪

考虑二进制每一位 $0/1$ 表示是否经过该点, 设 $dp_{i, j}$ 表示状态为 $i$, 最后停在 $j$, 转移枚举从哪个点到 $j$ 的.

注意初始化

1
2
for (int i = 1; i <= n; i ++)
    f[i][1 << (i - 1)] = dist(dots[i], dots[0]);

枚举状态转移

1
2
3
4
5
6
for (int j = 1; j < (1 << n); j ++)
    for (int i = 1; i <= n; i ++)
        if ((j >> (i - 1)) & 1)
            for (int k = 1; k <= n; k ++) 
                if (((j >> (k - 1)) & 1) && k != i)
                    f[i][j] = min(f[i][j], f[k][j - (1 << (i - 1))] + dist(dots[i], dots[k]));

轮廓线 $\rm dp$：一双木棋

手切 $\sout{2018}$ 联合省选 $\sout{\rm Day2\ T1}$

考虑使用状压记录当前轮廓线形状, 如 $1$ 表示向下的轮廓, $0$ 表示向右的轮廓, 每次转移时找到 $0$ $1$ 交界处转移即可. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
memset(f, 0xff, sizeof f);
f[((1 << n) - 1) << m] = 0;

int dp(int s, bool p) {
	if (~f[s]) return f[s];
	f[s] = p ? -INF : INF;
	int x = n, y = 0;
	for (int i = 0; i < n + m - 1; ++ i) {
		(s >> i & 1) ? x -- : y ++;
		if ((s >> i & 3) != 1) continue;
		if (p) f[s] = max(f[s], dp(s ^ (3 << i), p ^ 1) + a[x][y]);
		else f[s] = min(f[s], dp(s ^ (3 << i), p ^ 1) - b[x][y]);
	}
	return f[s];
}

状压拓展: 子集枚举

子集枚举的时间复杂度分析 $\text{for}\ \text{T} \in \text{S}$

首先枚举 $\text{T}$ 集合大小 $k$：$\sum \limits_{k = 0}^{n}$.

大小为 $k$ 的集合数量共有：$\binom{n}{k}$ 个.

大小为 $k$ 的子集数量共有：$2^k$ 个.

根据二项式定理, 得

$$
\sum \limits_{k = 0}^{n} \binom{n}{k} 2^k =
\sum \limits_{k = 0}^{n} \binom{n}{k} 1^{n - k} \cdot 2^k = ( 2 + 1 )^n = 3^n.
$$

$3^n$ 一般能过 $n \le 15$ 的数据.

计数类 $\rm dp$

整数划分

完全背包解

$f_{i, j}$ 表示从 $1 \sim i$ 中选并且总和等于 $j$ 的所有选法集合, 可得状态转移方程：

$$f_{i, j} = f_{i - 1, j} + f_{i, j - i}$$

类比于完全背包的一维优化, 优化后的状态转移方程：

$$f_j = f_j + f_{j - i}$$

1
2
3
4
5
6
7
8
int n, f[N];

cin >> n;
f[0] = 1;
for (int i = 1; i <= n; i ++)
    for (int j = i; j <= n; j ++)
        f[j] = (f[j] + f[j - i]) % MOD;
cout << f[n] << endl;

其他解法

状态表示

$f_{i, j}$ 表示所有总和为 $i$ , 并且恰好表示为 $j$ 个数的和的方案数集合

状态计算

将全集按照所有拆分成的数字分为：

  1. 拆分成的数字中最小值为 $1$
  2. 拆分成的数字中最小值不为 $1$
  • 那么如何表示这两种状态呢 ？

对于第一种情况, 如果将其中的一个 $1$ 删除, 则可以从前面的状态转移到此状态且并不影响总方案数, 则该状态表示为 $f_{i - 1, j - 1}$

对于第二种情况, 如果将所有数都减去 $1$ , 在能够从前面状态转移到此状态的前提下仍能保证集合中的数均为正整数, 则该状态表示为 $f_{i - j, j}$

则有：$f_{i, j} = f_{i - 1, j - 1} + f_{i - j, j}$

值得注意的是, 题目要求输出一个正整数 $n$ 的所有拆分方案, 而以上的状态转移方程仅限于正整数 $i$ 拆分为 $j$ 个数, 因此对于所有方案的计算, 只需：

1
for (int i = 1; i <= n; i ++) ans += f[n][i];
$Solutions$
1
2
3
4
5
6
7
8
9
10
11
int n, f[N][N], res;
cin >> n;

f[0][0] = 1;
for (int i = 1; i <= n; i ++)
    for (int j = 1; j <= i; j ++)
        f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % MOD;
        
for (int i = 1; i <= n; i ++)
    res = (res + f[n][i]) % MOD;
cout << res << endl;

数位 $\rm dp$

  • 一般都是寻找特定区间内满足一定条件的数的个数.

另外, 由于数位 $\rm dp$ 转移较为麻烦, 因此常采用记忆化搜索的方式.

记忆化搜索函数传入的参数:

  • 枚举到的数字位数 $pos$
  • 最高位限制 $lim$
  • 前导 $0$ $zeo$
  • 另外的参数视题目而定

例题

数位和整除原数

较难的状态设计

环形 dp 与后效性处理

Other Articles
cover
最小生成树 | 学习笔记
  • 23/01/20
  • 21:16
  • 图论
cover
最短路算法 | 学习笔记
  • 23/01/17
  • 15:42
  • 图论
© 2022- 2025 GrainRain
Article table of contents TOP
  1. 1. 进阶动态规划与常见题型
    1. 1.1. 区间 $\rm dp$
      1. 1.1.1. 石子合并
        1. 1.1.1.1. 状态表示
        2. 1.1.1.2. 时间复杂度分析
        3. 1.1.1.3. $Solutions$
    2. 1.2. 树形 $\rm dp$
      1. 1.2.1. 典例 $1$ - 树的直径
        1. 1.2.1.1. 简化题意
        2. 1.2.1.2. $Solution$：
        3. 1.2.1.3. $Code$
        4. 1.2.1.4. 扩展: 寻找直径必经边 SDOI2013 直径
      2. 1.2.2. 典例 $2$ - 树的中心
        1. 1.2.2.1. 简化题意
        2. 1.2.2.2. $Solutions$
        3. 1.2.2.3. $Solutions$
      3. 1.2.3. 典例 $3$ - CF685B - 树的重心
        1. 1.2.3.1. 简化题意
        2. 1.2.3.2. $Solution$
      4. 1.2.4. 典例 $4$ - 最大独立集问题：没有上司的舞会
        1. 1.2.4.1. 简化题意
        2. 1.2.4.2. $Solution$
    3. 1.3. 状压 $\rm dp$
      1. 1.3.1. 经典模型
        1. 1.3.1.1. 旅行商问题：吃奶酪
        2. 1.3.1.2. 轮廓线 $\rm dp$：一双木棋
      2. 1.3.2. 状压拓展: 子集枚举
        1. 1.3.2.1. 子集枚举的时间复杂度分析 $\text{for}\ \text{T} \in \text{S}$
    4. 1.4. 计数类 $\rm dp$
      1. 1.4.1. 整数划分
        1. 1.4.1.1. 完全背包解
        2. 1.4.1.2. 其他解法
    5. 1.5. 数位 $\rm dp$
      1. 1.5.1. 例题
        1. 1.5.1.1. 数位和整除原数
    6. 1.6. 较难的状态设计
    7. 1.7. 环形 dp 与后效性处理
      1. 1.7.1.
Please enter keywords to search
  • to close